next up previous contents
Next: Solutions for waves at Up: Complex Represenation of Waves Previous: Introduction   Contents


Complex representation for traveling waves

To introduce the use of the complex representation for waves, we first consider a sinusoidal pulse of the form

\begin{displaymath} f(u) = A \cos(k u+\phi_0) = {\mbox{Re\,}}\left(\underline{A} e^{i k u}\right), \end{displaymath} (1)

where $\underline{A} \equiv A e^{i \phi_0}$ is a complex amplitude. Note that (1) is in exactly analogous form to what we did previously in the time domain for simple harmonic motion. The only difference is that now we are in the space domain, so that instead of angular frequency $\omega$ and time $t$, we use wave vector $k$ and position $u$.

Next, we consider the form of a traveling wave solution made from such a pulse,

$\displaystyle s(x,t)$ $\textstyle =$ $\displaystyle f(x-c t)$  
  $\textstyle =$ $\displaystyle {\mbox{Re\,}}\left(\underline{A} e^{i k (x-ct)}\right)$  
  $\textstyle =$ $\displaystyle {\mbox{Re\,}}\left(\underline{A} e^{i k x} e^{-i c k t}\right)$  
  $\textstyle =$ $\displaystyle {\mbox{Re\,}}\left(\underline{A} e^{i k x} e^{-i \omega t}\right)$  
  $\textstyle =$ $\displaystyle {\mbox{Re\,}}\left(e^{-i \omega t} \underline{A} e^{i k x} \right)$  
  $\textstyle =$ $\displaystyle {\mbox{Re\,}}\left(e^{-i \omega t} \underline{Q}(x) \right),$ (2)

where we have used the dispersion relation $\omega = c k$ and defined the complex amplitude at position $x$ to be
\begin{displaymath} \underline{Q}(x) \equiv \underline{A} e^{ikx}. \end{displaymath} (3)

The final line above shows that the motion at each point $x$ in such a traveling wave is just simple harmonic motion in time at the wave frequency $\omega$, with an amplitude and phase determined by $\underline{Q}(x)$. Specifically,

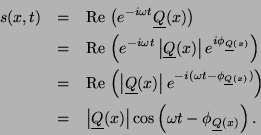
\begin{eqnarray*} s(x,t) & = & {\mbox{Re\,}}\left(e^{-i \omega t} \underline{Q}(... ...ert \cos\left(\omega t-\phi_{\underline{Q}(x)}\right). \nonumber \end{eqnarray*}



Thus, $\underline{Q}(x)$ determines completely the motion of point $x$ as simple harmonic motion with amplitude $\left\vert\underline{Q}(x)\right\vert$ and phase $-\phi_{\underline{Q}(x)}$. In the next section, we will find that the solution for wave propagation problems with input waves at a fixed frequency $\omega$ always has the form (2), so that determining the solution for the motion of the system boils down just to finding the complex wave amplitude function $\underline{Q}(x)$.

An important way of understanding the complex amplitude function $\underline{Q}(x)$ is to consider changes in the motion of a wave wave relative to its motion at a reference point $a$. To do this, we rewrite (2) as

\begin{displaymath} s(x,t) = {\mbox{Re\,}}\left( \left[ e^{-i \omega t} \underline{A} e^{i k a} \right] e^{ik(x-a)} \right), \end{displaymath} (4)

where the term in square brackets represents what we would have for the motion at the point $a$, and the factor $e^{ik(x-a)}$ represents the change in the motion in going from the point $a$ to the point $x$. Because the motion at all points is simple harmonic, the only possible differences in the motion as we go from point to point are in the amplitude or in the phase of the motion.

In the plane wave motion we consider here, a traveling wave moves along as a fixed shape, and so we expect the amplitude of the motion, (max - min)/2, to be constant for each point in space. (As waves spread outward from a point, as in the next set of notes, we in general can expect a decay in amplitude with distance.) The constantness of the amplitude corresponds to the fact that the propagation factor $e^{ik(x-a)}$ has amplitude $\left\vert e^{ik(x-a)}\right\vert=1$. Next, we generally do expect there to be a change in phase when moving from the point $a$ to the point $x$ because there is a time delay for maxima passing $a$ to reach $x$. The time delay for traveling the distance $L=x-a$ is $L/c$. To convert this to a phase in radians, we measure the delay in periods and multiply by $2\pi$: $\Delta \phi=2 \pi (L/c)/T=(\omega/c) L=k L$, precisely the phase appearing in the phase factor $e^{ik(x-a)}$. Thus, the propagation factor $e^{ik(x-a)}$ corresponds precisely to the phase delay as wave peaks pass $a$ propagating along to $x$. Note that the above argument is unaffected by whether the distance $L$ is traveled from left to right or from right to left. We thus have the following rule,

Propagation factor:
The effect of propagating a wave a distance $L$ (measured as a positive value whether the wave moves to the right or left) appears in the complex representation as multiplication by the complex phase factor $e^{ikL}$. For plane waves and waves moving in one dimension, this is the only factor. If the wave spreads out from a point in two or three dimensions, there in general may also be an amplitude decay factor.

next up previous contents
Next: Solutions for waves at Up: Complex Represenation of Waves Previous: Introduction   Contents
Tomas Arias 2003-10-27