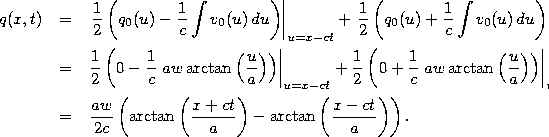Particular solutions from initial conditions

Suppose that we are given the value and velocity of the wave at time t=0: and , and we wish to determine q(x,t) the form of the wave at any time t later. To do this we follow the three-step procedure above.

1. Write each condition in terms of the general solution --

   The general solution is

    

   In terms of this, the first initial condition is

    

   and so we learn that the sum of the two unknown functions gives us the initial configuration of the system. The second condition is

    

   and so we learn that the wave speed times the difference of the derivatives of the two unknown functions gives us the initial velocities throughout the system.

   Interpretation of the two results (7,8) sometimes causes confusion because the variable t appears in the general solution (6) but not in the results. The best way to understand our results is to think of (7,8) as giving relationships between the various adjustable parameters, values of the the functions f() and g(). Eq. (7), for instance, says that when adding the values f(3) and g(3), one gets , and so forth for all possible values. Speaking very generally, and not thinking specifically about points in space, we could have used any value u in place of the number 3. Thus, a less confusing way of thinking about (7) would be to write

    

   so that we don't get hung up thinking about positions in space x or time t. Similarly, to avoid confusion, it is best to write (8) as

    

2. Solve the resulting set of equations for the adjustable parameters --

   For waves, the functions f() and g() give the adjustable parameters, and so for this step, we must solve (9) and (10) for f(u) and g(u).

   We begin by simplifying (10). Integrating both sides with respect to u, we find

    

   where C is a constant of integration and is the anti-derivative of the function .

   Now, by adding and subtracting, respectively, the two equations (9) and (11), we find

   

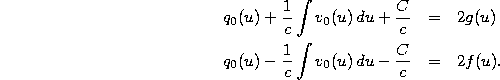
   Finally, dividing through by 2, we have the two unknown functions,

    

3. Write down the general solution while substituting the particular values found for the adjustable parameters --

   Substituting the results (12) into the general solution, we find

    

   where the unknown integration constant C has canceled out conveniently.

The result (13) is somewhat abstract. To learn how to use it, consider an example of a string which is initially ``flat'' (y(x,t=0)=0 for all x), but which has been given an initial ``kick'' near the origin so that the initial velocity distribution is . Now, to use (13), we need the following integral,

 

We also need the initial displacement, which was just zero in this case, . Substituting this and the integral (14) into the solution (13), we get the final result,