As another example of use of the general solution, we now consider an
important wave phenomenon, reflection from a boundary. Consider the
situations in Figures 2a and b, in which an initial
left-ward pulse of shape h(x) heads toward a boundary at x=0 with
either fixed (q(x=0,t)=0) or free ( 
)
boundary conditions, respectively.
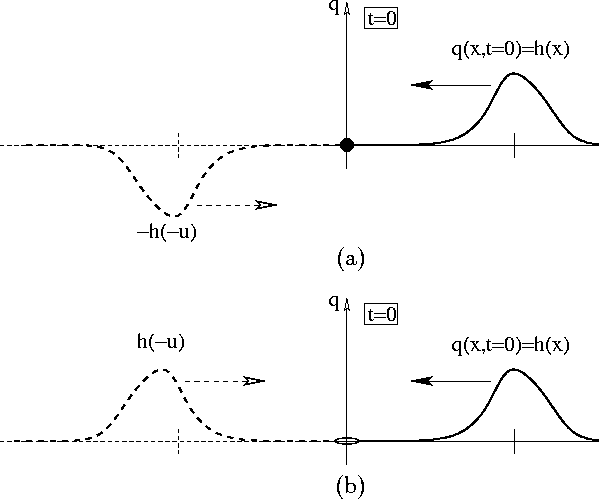
Figure 2: Reflection of an incoming left-ward pulse of shape h(x)
from a boundary at x=0: (a) fixed boundary, (b) free boundary
In order to determine what the system will do at later times, we use the fact that the general solution, by definition, describes all possible behaviors of the string. Thus, we know that the equation
describes behavior of the string at any later time t. (Note that whatever this equation gives for x<0 is just a mathematical fiction as the system ends at the boundary at x=0.) Our task, therefore, reduces to finding the values of the unknown functions f(u) and g(u) at all possible values of their argument u. Again, we use ``u'' instead of ``x'' to remind ourselves that the values f(u) and g(u) for each u really are unknown parameters and not tied to any particular point in space or time.
To find the unknown functions, we again use the initial conditions. There is now an additional condition which we must take into account, however. Recall that the presence of a boundary implies that the point on the boundary does not obey the same equation of motion as the other points, but rather a special equation which we called the boundary condition. This means that the general solution to the wave equation (15) applies everywhere but on the boundary and so we must take the boundary condition
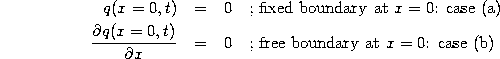
into account explicitly as an addition condition.
The initial condition was simply the presence of a left-ward moving pulse of shape h(x). This we will get if we take g(u)=h(u) because the second term of our solution will then be g(x+ct)=h(x+ct), a left-ward moving pulse of shape h(u). We thus have left only to find f(u), which we do by writing the boundary condition explicitly in terms of our general solution.
For the case of a fixed boundary, using the fact that we already know that g(u)=h(u), we find
To understand the meaning of the change of variables, note that Eq. (16) just says, for instance, that 0=f(-3)+h(3), and so, therefore, f(-3)=-h(3). Or that 0=f(5)+h(-5), and thus f(5)=-h(-5). The change of variables just allows us to say that this holds for all values, not just -3 and 5.
The interpretation of (17) is that, for this case of a fixed boundary, there is also a right-ward moving pulse (i.e., a reflection) which the boundary generates. The shape of the reflection, as Figure 2a illustrates, is just the same as that of the incoming pulse, except that it is up-side down (the first minus sign in (17)) and left-right inverted (the second minus sign in the equation). To complete the solution for the case of a fixed boundary, we substitute our results for f(u) and g(u) into the solution (15). In doing this, we note that (17) says that when we want the value of f(u) at any point u, whether u be -3, 5 or x-ct, we just put -h(-u). Thus, the solution for reflection from a fixed boundary is
The case of a free boundary is similar, but somewhat more complicated because of the derivative in the boundary condition. Following the same procedure of substituting our solution into the boundary condition, we find
Here, we again make the convenient substitution that u=-ct. Finally, we must solve (20) for the unknown function f(u). This we do by taking the anti-derivative,
which is easily checked by taking the derivative with respect to u
and recovering (20). To determine the unknown
integration constant C, we can play our usual trick and note that
and that we also expect 
, and so,
when we evaluate our solution for f(u) at either of these points, we
find that C=0. Thus, for free boundary conditions, we conclude that
the reflected pulse is
which means that the reflection, as Figure 2b illustrates, is now right-side up (no initial minus sign) and still left-right reflected (minus sign inside h()). Once again, we substitute into (15) to get the final solution for reflection from a free boundary,
