We now consider the simplest case which exhibits interference, two
equivalent, narrow slits (Figure 3). Of course, you
can get the two-slit pattern by substituting N=2 into the formula we
shall eventually derive for N slits. But, deriving the two slit
result as a special case first allows us to illustrate several useful
results and techniques for complex arithmetic that you will have to
master, in particular computing the amplitude of the complex number
with the formula 
. This section appears very mathematical because we show
all of the steps. As you learn to do these steps, they will
become simpler and simpler for you.
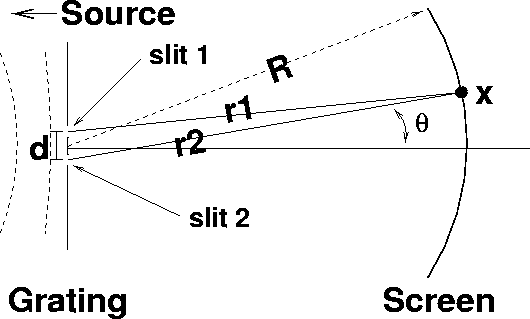
Figure 3: Double-slit interference experiment
According to our main result, Eq. 8, the intensity at a
point 
on the screen for just two slits is
where 
and 
, 
and 
, and 
and 
,
respectively, are (a) the intensities which each slit (if alone) would make
at point , (b) the phases of the waves emerging from each
slit, and (c) the distance from each slit to the point .
Now, because we assume the two slits to be equivalent, they must let
the same intensity of waves through, and so the intensities which each
separately would create on the screen are very nearly the same, so
that 
. (There will be a slit difference in the
distance from each slit to the point on the screen, but so
long as the screen is much further away than the separation of the
slits, R>>a, this difference is negligible.) For simplicity, let us
call this intensity which either slit alone creates on the screen
.
Next, because the waves coming from behind the diffraction grating
arrive at both slits in phase (Figure 3), the
phases of the waves coming out of the slits will be equal,
. For simplicity, let us call this phase 
. As
we shall see in a moment, the fact that these phases are equal means
that they cancel from the final result. Note that this is only true
if the waves coming from behind the grating arrive at the slits with
equal phases!
Putting this all together we have,
where, again, we have used the facts that 
and 
for any complex phase factor.
Note that, as we had mentioned, in the end, the phases indeed cancel
out. Also note that the entire result now depends only on the
difference in lengths between the paths from the observation point to
each slit, 
.
The entire computation of I now boils down to finding 
. A very useful way to find the
square-magnitude of a complex number is to use the
following fact
where, for any complex number , we define the
complex conjugate as 
.
Mathematically, taking the complex conjugate simply amounts to finding
all occurrences of i and substituting 
.
Using the procedure of Eq. 12, we now find
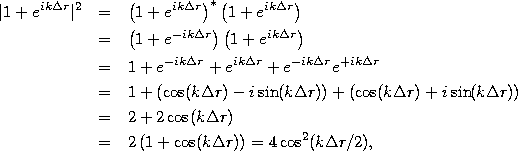
where on the last line we find a somewhat simpler form by using the
trig identity 
. Combining this
with Eq. 10, we have the final result for two-slits,
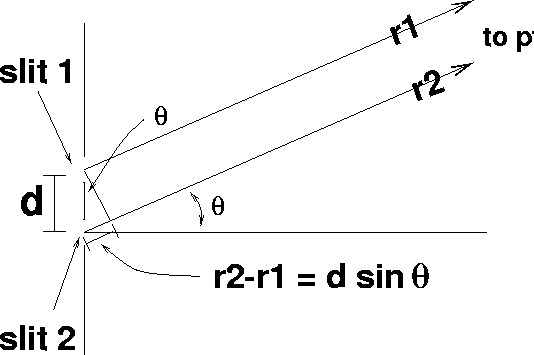
Figure 4: Double-slit interference experiment: enlarged view
All that remains is for us to learn to compute the path
difference 
. Figure 4 shows
that the path difference 
corresponds very closely to the
opposite side of a right triangle of angle 
and hypotenuse
d. Accordingly, our final result is Eq. 13 with the
definition
