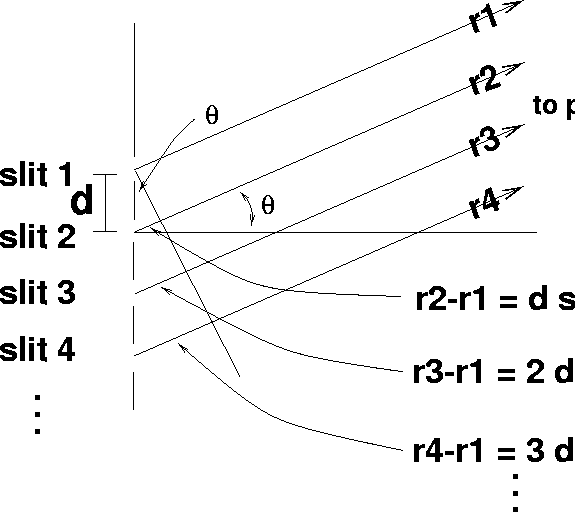
Figure 6: Interference experiment with N finite slits
We now use all of the skills we have developed to derive what happens in the case of N identical, very narrow slits, all at equal separations d from one another (Figure 6). The only new technique in this section is that we use the formula for the sum of a geometric series.

Figure 6: Interference experiment with N finite slits
Following our derivation for the two-slit case, we begin with
![]()
where we already have used the fact that all slits let through the
same intensity (all I's are equal) and waves arrive at the slits and
thus emerge from them all with the same phase (all ![]() 's are the
same).
's are the
same).
Once again, we can factor out the constant phases, and the intensity we would expect from each slit individually, leaving only a sum of exponentials of path differences times k,
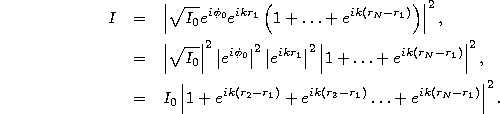
The next key step is to realize that the path differences are just
multiples of each other. If we define, again, ![]() , then
, then ![]() ,
, ![]() ,
,
![]() ,
, ![]() . (See Figure 6.) Thus, we must
compute the sum
. (See Figure 6.) Thus, we must
compute the sum
![]()
but this is just a geometric series ![]() with geometric ratio
with geometric ratio ![]() . The formula you know for real numbers, G=1/(1-r) still works,
and so the sum is
. The formula you know for real numbers, G=1/(1-r) still works,
and so the sum is
![]()
To compute the magnitude of this, we use the fact that the magnitude
of the ratio is the ratio of the magnitudes. Then, we note that both
numerator and denominator have the same form, ![]() , where for
the former case
, where for
the former case ![]() and for the latter
and for the latter ![]() . For both cases, we have
. For both cases, we have
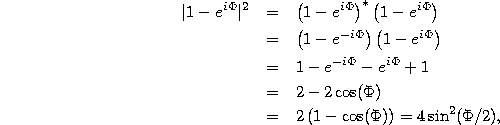
where, again, at the last step we use a convenient trig identity. Using this, our final result is
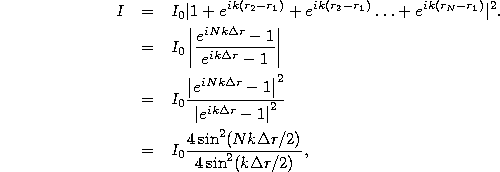
which simplifies to our final result,
where, as before, ![]() .
.