



Next: Finite slit: Diffraction
Up: N narrow slits
Previous: Analysis
Again, several features of our result, Eq. 17, are
noteworthy. Figure 7 shows this result for a case
with N=6 slits.
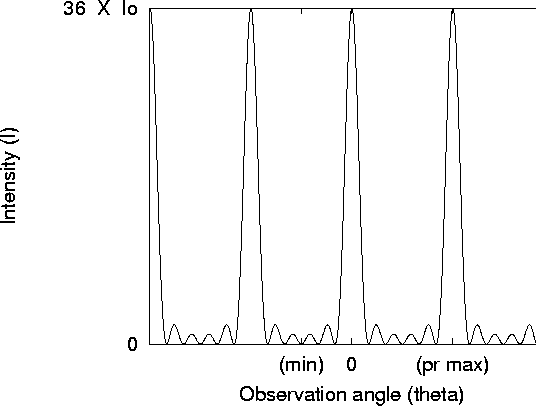
Figure 7: Intensity as a function of observation angle for an N-slit
experiment for the case N=6. In this case, principle maxima appear
in the location of every sixth minima, so that there are five minima
between principle maxima, and thus four lesser maxima between
principle maxima.
- Case of two slits: If we substitute N=2 into
Eq. 17 and use the double-angle sine formula, we have for
the numerator
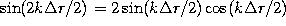 , so that the
, so that the  term in the denominator cancels,
leaving
term in the denominator cancels,
leaving 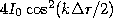 , precisely the two-slit result,
Eq. 13.
, precisely the two-slit result,
Eq. 13. - Principle maxima: we find extremely large maxima whenever the
denominator in Eq. 13 goes to zero. This occurs
whenever
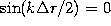 , equivalently,
, equivalently, 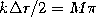 ,
where M is some integer. This means
,
where M is some integer. This means
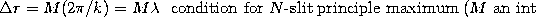
so that the path difference between all of
the slits is always an exact number of wavelengths, leading to
complete constructive interference. To see how large the maxima can
be, we take the limit 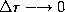 . From the
small-angle formula, we then have
. From the
small-angle formula, we then have

The physical reason for the factor of 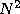 is just that the amplitudes of all
N waves add, so the amplitude is N times as large, but
the intensity, of course, goes like the amplitude squared.
is just that the amplitudes of all
N waves add, so the amplitude is N times as large, but
the intensity, of course, goes like the amplitude squared.
- Minima: Minima occur in the pattern whenever the numerator is
zero (and the denominator is not). Zeros in the numerator occur
whenever
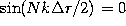 , equivalently,
, equivalently, 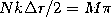 , where M is any integer, so that
, where M is any integer, so that
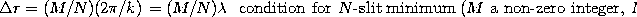
Note that the spacing between minima is thus exactly
1/N times the spacing between principle maxima. Often, you can use
this to determine the number of slits from the appearance of the
diffraction pattern.
- Lesser maxima: Of course, there are other maxima which must
appear approximately halfway between neighboring minima, the
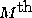 of these happens
where
of these happens
where
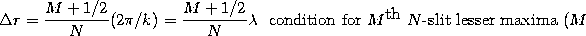




Next: Finite slit: Diffraction
Up: N narrow slits
Previous: Analysis
Tomas Arias
Thu Sep 13 15:26:14 EDT 2001
