



Next: About this document
Up: N finite slits: combining
Previous: Analysis
Figure 11 shows the result for a case where the
spacing between slits d is exactly three times the width of the
slits. Among many interesting features, two are noteworthy in this
result.
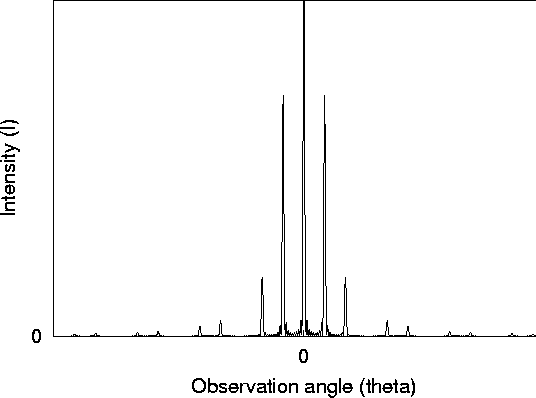
Figure 11: Intensity as a function of observation angle for an
experiment with N slits of finite width, where N is large (N=10)
and the slits are spaced four times further apart than they are wide,
d/a=3. Note how this pattern has every third principle maxima
(except the central maximum) wiped away.
- Spacing between maxima: Because
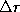 is larger (d, the
spacing between slits, must be larger than a, the width of the
slits, otherwise the slits overlap!), the most rapid oscillations come
from the N-slit interference pattern, which then sets the basic
pattern. Note that if N is large (N is only ten in the figure),
then you see mostly the principle maxima. The little fuzz in the
figure hardly visible near zero are the lesser maxima and would
become nearly invisible for any large value of N. This is a general
feature of the N slit pattern and not particular to the case of
finite slits!
is larger (d, the
spacing between slits, must be larger than a, the width of the
slits, otherwise the slits overlap!), the most rapid oscillations come
from the N-slit interference pattern, which then sets the basic
pattern. Note that if N is large (N is only ten in the figure),
then you see mostly the principle maxima. The little fuzz in the
figure hardly visible near zero are the lesser maxima and would
become nearly invisible for any large value of N. This is a general
feature of the N slit pattern and not particular to the case of
finite slits! - Missing Principle Maxima: The main impact from the finite width
of the slits is that it changes the amplitude of the principle maxima.
Rather than having equal heights, the height of each maximum is
multiplied by the finite-slit factor in Eq. 20.
We
expect the N-slit pattern (Section 3.3.2) to have
principle maxima wherever
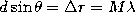 , where
M is an integer, so that
, where
M is an integer, so that 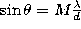 .
However, these maxima can sometimes be wiped away by the finite-slit
diffraction factor in Eq. 20. In particular, the
zeros of the finite-slit diffraction pattern occur where
.
However, these maxima can sometimes be wiped away by the finite-slit
diffraction factor in Eq. 20. In particular, the
zeros of the finite-slit diffraction pattern occur where 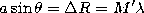 , or
, or 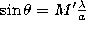 ,
where M' is another integer. Whenever both of these conditions are
met at once, we find that the
,
where M' is another integer. Whenever both of these conditions are
met at once, we find that the 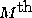 expected maximum appears
to be missing.
expected maximum appears
to be missing.
Equating 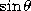 in both cases, we find that this happens when
in both cases, we find that this happens when

is an integer. In our example, a/d=1/3, and so we expect every third
principle maximum M (except the one in the center, M=0) to be missing,
exactly as in Figure 11!




Next: About this document
Up: N finite slits: combining
Previous: Analysis
Tomas Arias
Thu Sep 13 15:26:14 EDT 2001
