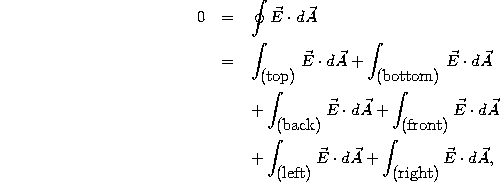
We have not yet said anything of the polarization of E&M waves. This is because such a determination requires us to consider the governing physics, namely (14-17). In particular, Gauss's laws (14) and (16) determine the nature of the polarization of electromagnetic waves.
The Gaussian ``pillbox'' in Figure 4 allows us to apply these laws to a plane wave traveling along x. Considering first the electric field, Eq. 14 tells us
where we have broken the closed surface integral around the pillbox into the sum of flux integrals over each of its faces. From the fact that we have a plane wave and thus that the electric field is constant in each plane (such as x' in the figure), we see that (a) the electric flux entering the bottom of the pillbox equals exactly the electric flux exiting the top and that (b) the flux entering the front equals exactly the flux exiting the back. Thus, the top and bottom integrals sum to zero and the back and front integrals sum to zero. This leaves
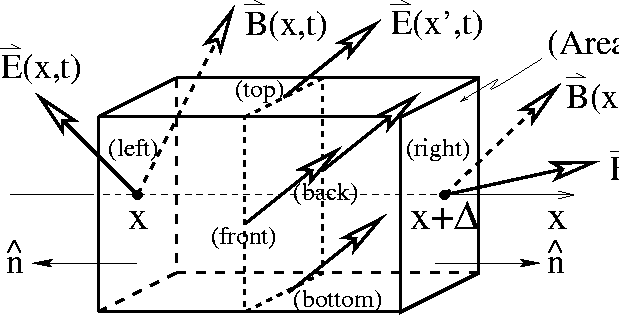
Figure 4: Pillbox for application of Gauss's laws to a plane wave
traveling along the x direction.
Due to the nature of the plane wave, we are fortunate in evaluating
the remaining integrals over the left and right faces because the
electric field is constant over each. In both
cases, we take the dot product of the electric field with the outward
normal vector to the surface 
and multiply by the area A.
As indicated in the figure, the normal vector to the left face is
and to the right face is 
. Substituting this into
(21) and simplifying,
where we have used the fact that the components of any vector may be
obtained by dotting with the corresponding unit vector: 
, 
, 
.
Eq. 22 tells us that the x-component of 
is
constant. To determine the value of this constant, we do as we did
with the x-component of the tension in the string and consider the
value of 
at the edge of the system. Unlike the string, in this
case our system has no actual end and extends off to infinity. Very
far from the sources of any fields, we expect the fields and
to be zero. Thus the value of the constant is zero and so
The fact that the x component of is zero is best summarized
by saying that is perpendicular to the direction of
propagation. In other words, the electric field in an electromagnetic
wave is transversely polarized.
Turning next to the magnetic field, we now apply
(16). Note that (16) is
identical to (14) but with replacing .
Thus, the analysis for the magnetic field will follow exactly the same
logic and generate Eqs. 21-23 but with
E replaced everywhere by B. Thus, we conclude
and that both the electric and magnetic fields in an electromagnetic wave are transversely polarized.
