Having determined the polarization, we turn next to the equations
describing laws of motion of the fields,
(15) and (17), and express them in terms of
the solution ( 
and 
), its derivatives and
fundamental constants. Figure 5 shows the Amperean
loop which we shall use to study these laws.
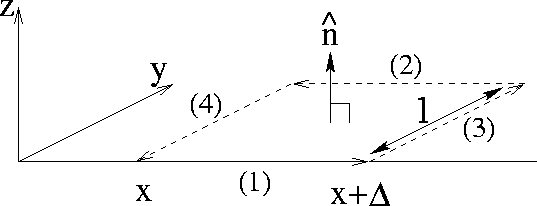
Figure 5:
Amperean loop for application of Ampere's and Faraday's
laws to a plane wave traveling along the x direction.
Applying Ampere's law (15) to this loop, we find
Here, we have broken the Amperean loop into the four segments in the
figure and used the fact that the magnetic field is transversely
polarized and thus 
along sides (1) and
(2). Again, we are fortunate in that along each of the contributing
integrals, sides (3) and (4), the field 
is constant. Thus,
for these integrals, we have just the dot product of the value of
with the corresponding direction times the length 
of
the side. As sides (3) and (4) are along 
and 
, the
dot products pick out the y component of the field 
. As
for the right-hand side of (25), 
is oriented
perpendicular to the loop according to the right-hand rule and thus is
along the direction 
in the figure. Finally, the
total area of the loop is 
. Putting this all
together, we find
Here, the only subtlety is that the value of 
is not constant
across the face of the loop. Thus, what we find for the integral is
the average value of times the area of the loop. This is
much akin to what we found for the string and for sound where we end
up with an equation involving the location of the center of mass of a
chunk of the system. The resolution of this, as in the other two
cases, is to take the limit 
so that the loop
shrinks down to the point x so that the average value just becomes
the value at x at the particular point in time, 
. Taking the limit, Eq. 26 thus
gives our first law of motion
Turning next to Faraday's law (17), we can repeat the
same procedure. For this analysis, we note that Faraday's law (17) looks just like
Ampere's law (15) but with 
replaced with
and with 
replaced with 
. Thus,
the derivation for Faraday's law will just repeat
Eqs. 25-27 but with the aforementioned
replacements at each and every step, leading to the final result
As we have four unknown degrees of freedom ( 
--
From the polarization we already know that 
.), we shall
require four equations. The other two equations come from considering
the loop in the xz plane shown in Figure 6. The
analysis will follow exactly as before with (25) with
the loop integrals along (1) and (2) being zero because the fields are
transverse but with the integrals along (3) and (4) now picking out
the z-components 
. The area integral for
also works similarly, but now because 
points along ,
the right-hand side picks up an extra minus sign. Our final result
looks like (27), but with these changes:
For the final equation, we apply Faraday's law to the second loop. Making the same changes which we made above to generate Faraday's law from Ampere's law for the first loop, we find
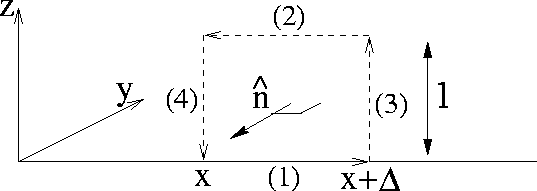
Figure 6: Second Amperean loop for application of Ampere's and Faraday's laws
to a plane wave traveling along the x direction.
