To derive the equation of motion, we begin by writing Newton's law for
the chunk of gas (or liquid or solid) sketched in
Figure 3. As with the string, we ignore long-range forces
as either irrelevant (electromagnetic) or insignificant (gravity).
The only contact forces come from neighboring chunks. We describe
this contact force through the pressure P, defined as the
force per unit area, acting across each face of the chunk. Pressure
defines how much the neighboring chunks push on the chunk we
have under consideration. Thus, as the figure indicates, the pressure
force on the right-hand face points to the left whereas the pressure
force on the left-hand faces points to the right. Finally, the
passage of sound will change the pressure in the gas, and so we shall
use 
to denote the pressure of the gas in the absence of any
disturbance.
To describe the mass associated with the gas we shall use the
density 
, defined as the mass per unit volume, and we shall
define 
as the density in the absence of any disturbance. To
determine the mass 
of the chunk in Figure 3, we
exploit conservation of mass and consider the mass of the chunk in its
initial configuration in the absence of any disturbance, where it has
density , cross-sectional area A, and width 
. Thus,
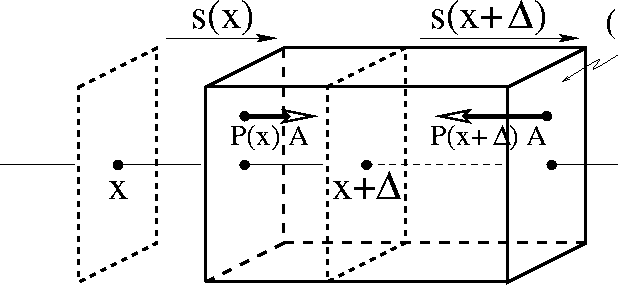
Figure 3: Free body diagram for pressure wave:
present (solid planes) and initial (dashed planes)
boundaries for chunk.
Focusing on motion in the x-direction (corresponding to our degrees of freedom) and using Newton's law for finite bodies, we find
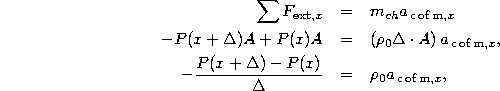
where in the last step we have canceled the common factors A and
divided through by . Finally, in the limit 
, the left-hand side becomes the partial derivative
, and the chunk shrinks down to the point x so
that its acceleration becomes the same as the acceleration at the
point x: 
(Eq. 3). Combining these two results for
the limit, we have
which gives the law of motion for the chunk.
Note the similarity of (5) to the corresponding equation for the string. We have the first partial spatial derivative of the driving force equal to the product of a measure of the inertia and the acceleration of each chunk. The derivative represents the sum of the forces, which are in opposite directions on either side of the chunk and thus appear as a difference. The product of the measure of the inertia and the acceleration of each chunk represents the ma side of Newton's equation and ensures that the chunk's acceleration is directly proportional to the net driving force and inversely proportional to the inertia. The difference in signs of the left-hand sides between the sound and string laws of motion comes simply from the fact that pressures always push whereas tensions always pull. Otherwise, the equations are completely analogous.
Finally, following our analysis of the string, it can also be useful
to consider the momentum density, in this case the momentum per unit
volume. This momentum density is the product of the mass per
unit volume and the velocity, 
,
We can then rewrite (5) as relating the net flow of momentum into each chunk to the time rate of change of its momentum,
