Figure 5 shows our physical realization of a damped,
driven harmonic oscillator. Note that the system is very similar to
the simple harmonic oscillator in Figure 1. The
only new physical forces at work are the driving force 
with magnitude 
, initial phase 
and frequency 
, and a viscous drag force 
which is in direct proportion but oppositely oriented to the velocity,
always tending to slow or damp the motion.
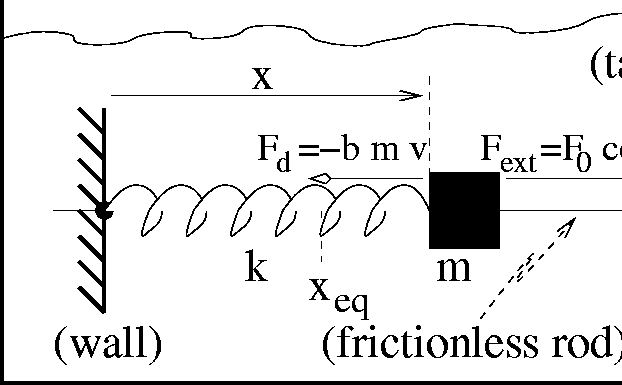
Figure 5: Damped, driven simple harmonic oscillator: spring-mass system
with an external driving force and damping
We consider damping in this problem because (a) all realistic physical
systems involve some sort of damping, (b) while damping may be ignored
in many applications, it becomes particularly important when we drive
at the natural frequency and thereby generate large, rapid motions.
Note that we write the damping coefficient as b m purely as a
mathematical convenience. If you prefer, you can think of the drag
force as being 
, and then the value of b is simply
.
Finally, we use to indicate the driving frequency. This is
something entirely different from the natural frequency of the
oscillator 
, which we define with the
subscript ``0''.