Analysis

We now repeat the stages of our general analysis.

1. Degrees of Freedom (D of F): As with the simple harmonic oscillator, the only degree of freedom is x.
2. Equation of Motion (E of M): Starting from Newton's law and continuing until we have only x, derivatives of x and constants defined in the problem, we find

   

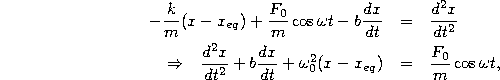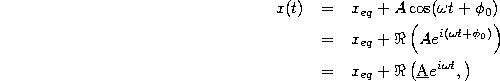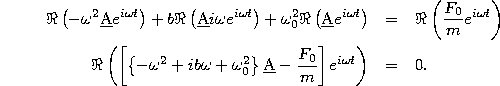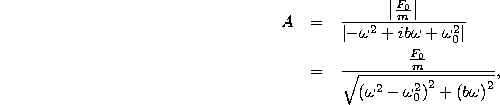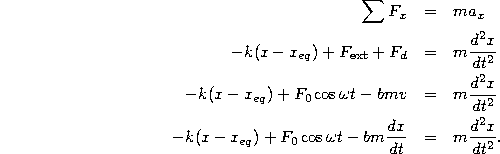
   This now is a valid equation of motion. Simplifying by dividing through by m and rearranging a bit, we find

    

   where we have defined the natural frequency of the system as as above in (7).

3. Solution: Here, we seek only a typical solution to the equation of motion. A reasonable guess is that the mass will oscillate about the equilibrium point at the driving frequency with some amplitude A and initial phase . As we anticipate the complex representation making our mathematical task much easier, we also express this guess solution in complex form. Our guess solution is therefore

    

   where, as above, we define .

   To verify this as a solution and to identify the appropriate value of , we substitute (36) into the equation of motion. As usual, we first evaluate the useful terms before substituting:

   

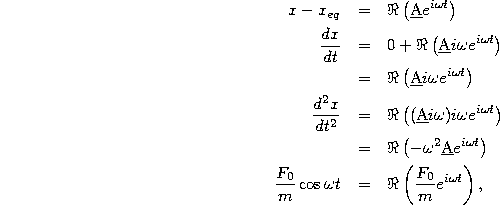
   where, in the last step, we use Euler's formula to get the driving force term into a form similar to all of the other terms. Substituting all of these terms into the equation of motion (34), and collecting terms we find

    

   To complete the argument, we note that the left hand side of (37) describes an oscillation of amplitude , whereas the right hand size is zero. This equation holds for all time t if and only if the amplitude of the oscillation on the left-hand size is zero. Thus, the equation of motion is satisfied by our solution, but only if

   

   or, solving for ,

    

4. Magnitude and Phase: From the result (41), we are now in a position to determine the amplitude and initial phase of the resulting motion. We know that these, respectively, are the magnitude and phase of the complex number . To simplify our work, we note that (38) has the form of a quotient of two complex numbers. The magnitude and phase of such a quotient may be determined simply from the following argument,

    

   where we have used the fact that complex numbers and always may be decomposed into amplitudes and phases, and . From the final line of (39), we learn two simple rules: (1) the magnitude of a quotient is the quotient of the magnitudes, and (2) the phase of a quotient is the difference of the phases. Mathematically,

   

   Thus, in our particular case,

    

   and,

    

   Figures 6 and 7 plot these results for the amplitude and initial phase, respectively.

     
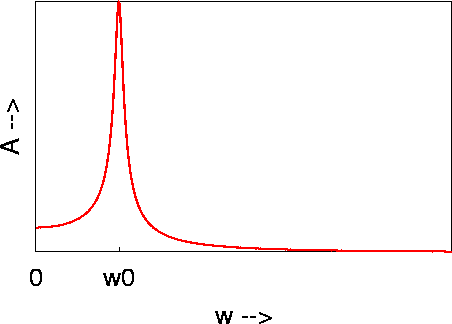
   Figure 6: Amplitude (A) of driven, damped harmonic oscillator as a function of drive angular frequency (w)
   

     
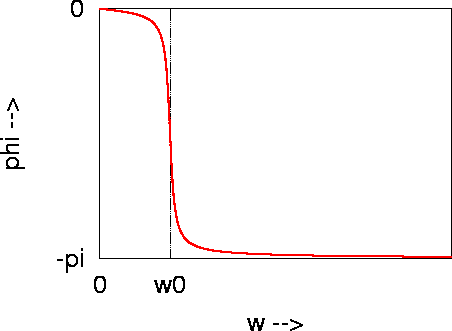
   Figure 7: Initial phase (phi) of driven, damped harmonic oscillator as a function of drive frequency (w)