We begin by considering the case of the string. All motion is then
along the y direction; hence, we need consider only momentum in the
y-direction, 
. The string is a d=1 dimensional system and we
therefore consider the linear momentum density 
, the momentum per
unit length. Momentum being mass times velocity, the momentum per
unit length is the mass per unit length 
times the velocity; hence,
plays the role of q in (2) when considering
conservation of momentum
.
Next, to understand the flow of momentum, we note that Newton's law for finite systems states
Thus, the rate of change of the total momentum of any system (such as
the chunk between points x and 
) is the sum of
external forces acting on it. As we have always ignored gravity (and
the other long-range forces) in our analyses, the only relevant
remaining forces are the contact forces at points x and .
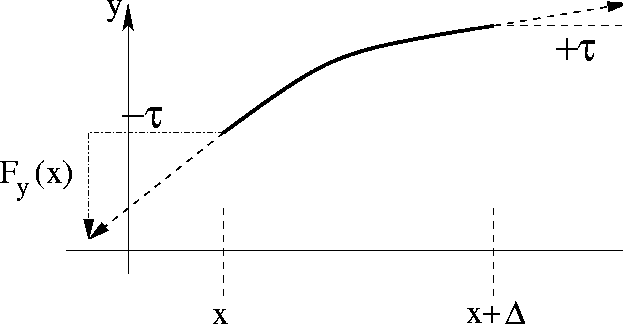
Figure 2: Momentum and energy flow via forces on a string
For the string (Figure 2), the contact force
at point x comes from the tension in the segment of the
string to the left, 
, and the force at point comes from the tension in
the segment to the right 
. Consistent with what we already
know about lack of x motion in strings, the x components of the
tensions cancel, leaving us to consider motion in the y direction
only. If we now define the quantity
for any point x, we may then write
Comparing (6) with (1), we see
that the quantity describing the left-right flow F(x) across point
x in (1) is nothing other than the y component
of the tension force 
, with the sign as in
(5). Thus, we may interpret force as describing the
rate of flow of momentum from one part of a system to another.
We are now ready to consider the continuity equation for momentum
along a string. The quantity from Eq. (4)
plays the role of q, the density of the conserved quantity, and the
quantity from Eq. (5) plays the role of F(x),
the rate of flow of the conserved quantity. Thus, if indeed
momentum is conserved for a string, we expect the following equation
to hold,
To verify whether this equation holds, we substitute our definitions (4,5) of the density and flow into (7) to find
which we know to be true because we recognize it as the wave equation for the string!!!
