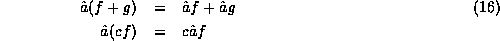
Defined according to the procedure in the discussion above, all of our physical operators have the mathematical property of linearity. This means that the action of a physical operator on a sum of functions is always equal to the sum of its action on each of the operators individually and that the action of an operator on a constant times a function is just that constant times the action of the operator on the function alone
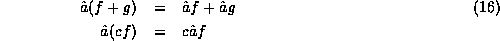
Moreover, all operators formed using the algebraic combinations of operator addition and multiplication from linear operators are also linear and thus all of the operators, with a single notable exception, you will encounter in quantum mechanics will be linear. The one exception to this is the ``time reversal'' operator, which you will learn about in a later course.
From the form of our physical operators, they are all clearly linear in the pure state representation associated with the operator, where the action of the operator is just multiplication by the argument of the function. Once we establish this, we will argue again that as we move to other representations, this statement preserves its mathematical form and so the property of linearity holds for any physical operator in any representation. Now, in the pure state representation, the operator clearly distributes over the sum of the functions,
Because of the manner in which we have defined the action of physical
observables in representations other than that of their pure states,
when we transform the above equation to any other representation, it
looks the same. If we take  , by the
principle of superposition we will have
, by the
principle of superposition we will have 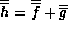 and if
and if
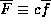 then
then  . Further, by
the definition of our operators
. Further, by
the definition of our operators  will be the
transform of
will be the
transform of 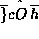 ,
, 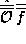 the transform of
the transform of
 and
and 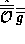 the transform of
the transform of
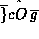 .
Thus, the transform of (17) is just the general statement
we wish to prove for any physical operator in an arbitrary
representation,
.
Thus, the transform of (17) is just the general statement
we wish to prove for any physical operator in an arbitrary
representation,

It is easily verified that the operators we have introduced so far are linear.

A simple example of an operator which is not linear is the
operator which add one to any function, 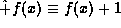 .
We would then have
.
We would then have
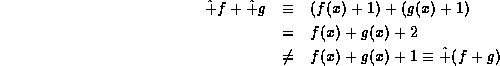
Because the  operator in not linear, we know immediately that
it does not correspond to any physical observable and thus may
immediately disqualify it as a
physical operator.
operator in not linear, we know immediately that
it does not correspond to any physical observable and thus may
immediately disqualify it as a
physical operator.
Finally, it is is easily verified that starting with physically observable operators (which we have just demonstrated all to be linear) and forming new combinations by operator addition and multiplication, the result is always another linear operator. This follow directly from induction and the facts that that the sum and operator product of two linear operators is always a third linear operator. These facts are verified directly below.

Thus we see that all operators which will concern us are linear. With this established, we may now freely exploit a second distributive law, which is companion to (11) and which follows directly from linearity,