


Next: About this document
Up: Quantum Operators
Previous: Hermitianness
While we have built up a powerful mathematical framework of function
operators, one in which the Heisenberg Uncertainty Principle may be
seen to follow directly, our framework is still open to the valid
criticism that our function operators are very clumsy, requiring an
entirely new set of operators for each new representation. In
practice, it is inconvenient to keep track of all of the tilde,
over-bar and double over-bar symbols when 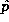 ,
, 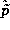 ,
,
 and
and  all refer to the same physical
observable. While for most of 8.04 we shall find it most convenient to
work nearly exclusively in just the position representation, the
student should be aware that in abstract discussions there is a more
powerful concept known as the quantum operator which deals
effectively with this criticism. A ``quantum,'' as opposed to
``function'' operator takes as its input a quantum state,
rather than a function, and returns as its output another quantum
state, as opposed again to a function. Symbolically, we will use
Dirac notation for this concept and write the action of a
quantum operator (which we shall always designate with the subscript
``op'')
all refer to the same physical
observable. While for most of 8.04 we shall find it most convenient to
work nearly exclusively in just the position representation, the
student should be aware that in abstract discussions there is a more
powerful concept known as the quantum operator which deals
effectively with this criticism. A ``quantum,'' as opposed to
``function'' operator takes as its input a quantum state,
rather than a function, and returns as its output another quantum
state, as opposed again to a function. Symbolically, we will use
Dirac notation for this concept and write the action of a
quantum operator (which we shall always designate with the subscript
``op'') 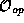 on a state
on a state 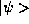 to produce the state
to produce the state
 as output as
as output as

The power of (22) is that its meaning is entirely clear
without reference to any particular choice of representation. To
evaluate (22) in practice, we may proceed in three
steps. 1) Write 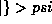 as a quantum amplitude in some
representation, for instance as a superposition in terms of the the
pure states of some observable
as a quantum amplitude in some
representation, for instance as a superposition in terms of the the
pure states of some observable 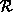 (not necessarily the same as
(not necessarily the same as 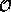 ),
),
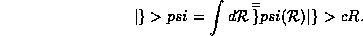
2) Apply the operator appropriate to the observable 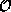 in this
representation to
in this
representation to  to produce
to produce  , and 3)
reconstruct the final quantum state from
, and 3)
reconstruct the final quantum state from  ,
,

We have been careful in the definition of our function operators so
that this procedure always results in the same quantum state
regardless of the representation 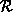 we choose, and we may thus
write (23) without ambiguity.
we choose, and we may thus
write (23) without ambiguity.
From our representation-free definition of the quantum inner product
and this new representation-free definition of quantum operators, we then
have a representation-free form for writing quantum averages,
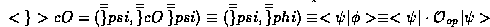

A particularly natural choice for the representation in which to carry
out (23) is with pure states associated with the
observable. This will lead us to a very compact definition of the
action of quantum operators known in terms of an eigenvalue equation.
We will discuss this special result not only because it is useful for
defining operators in abstract discussions but also because it gives
us a powerful practical method of recovering the quantum amplitudes
(wave functions) of pure states of an observable in arbitrary
representations when all we know about the observable
in these representations is the form of its operator.
To find the eigenvalue equation we proceed to write (23)
for an arbitrary state (described by an arbitrary set of amplitudes
 ) in
the pure state representation associated with
) in
the pure state representation associated with 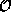 . Using the fact
that we know that the operator associated with the observable in that
representation is just multiplication by the argument we now have two
ways of writing the action of the operator on the state
. Using the fact
that we know that the operator associated with the observable in that
representation is just multiplication by the argument we now have two
ways of writing the action of the operator on the state 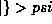 ,
,

From their definition through (23) we see that, like
function operators, quantum operators are linear (their action
on the sum of two states is the sum of their action on each states
individually). Noting further that quantum operators act only on
states and not on functions, we may then move 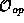 through the
integral above to conclude that for arbitrary
through the
integral above to conclude that for arbitrary  ,
,

Since this relation must be true for any  ,
,
 for instance, we must
have for all
for instance, we must
have for all  ,
,
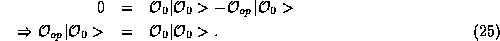
This gives us a completely general and representation-free definition
for the action of a quantum operator. This definition arises
ultimately from the physical fact that the square of
quantum amplitudes correspond to probabilities and our construction of
operators to give correct averages:
Definition: The action of a quantum operator on a pure state with
respect to the observable associated with the operator is just to
return the pure state of the observable multiplied by the value of the
observable in that state.
The form of the equation (25) is very common in
mathematics, it is known as an ``eigenvalue'' (or, sometimes
``characteristic'') equation of the operator. 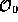 is called the
eigenvalue (characteristic value) and
is called the
eigenvalue (characteristic value) and 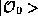 is the eigenstate
(characteristic state).
is the eigenstate
(characteristic state).
As mentioned above, we may use the eigenvalue equation to recover the
representation of all of the pure states of an observable in any
representation from only the form of the operator. As an example, if
our operator is the momentum operator and we are working in the
position representation, (25) becomes
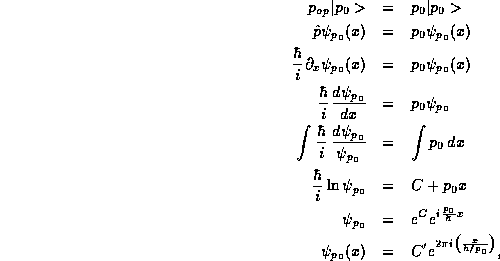
which apart from the undetermined constant of proportionality,  , is
just the de Broglie hypothesis that the pure state of momentum
, is
just the de Broglie hypothesis that the pure state of momentum  is a wave of wavelength
is a wave of wavelength 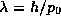 . We see that the first de Broglie
hypothesis is now built directly into our
operator framework!
. We see that the first de Broglie
hypothesis is now built directly into our
operator framework!



Next: About this document
Up: Quantum Operators
Previous: Hermitianness
Prof. Tomas Alberto Arias
Wed Oct 11 21:37:35 EDT 1995
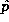 ,
, 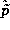 ,
,
 and
and  all refer to the same physical
observable. While for most of 8.04 we shall find it most convenient to
work nearly exclusively in just the position representation, the
student should be aware that in abstract discussions there is a more
powerful concept known as the quantum operator which deals
effectively with this criticism. A ``quantum,'' as opposed to
``function'' operator takes as its input a quantum state,
rather than a function, and returns as its output another quantum
state, as opposed again to a function. Symbolically, we will use
Dirac notation for this concept and write the action of a
quantum operator (which we shall always designate with the subscript
``op'')
all refer to the same physical
observable. While for most of 8.04 we shall find it most convenient to
work nearly exclusively in just the position representation, the
student should be aware that in abstract discussions there is a more
powerful concept known as the quantum operator which deals
effectively with this criticism. A ``quantum,'' as opposed to
``function'' operator takes as its input a quantum state,
rather than a function, and returns as its output another quantum
state, as opposed again to a function. Symbolically, we will use
Dirac notation for this concept and write the action of a
quantum operator (which we shall always designate with the subscript
``op'') 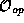 on a state
on a state 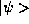 to produce the state
to produce the state
 as output as
as output as

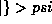 as a quantum amplitude in some
representation, for instance as a superposition in terms of the the
pure states of some observable
as a quantum amplitude in some
representation, for instance as a superposition in terms of the the
pure states of some observable 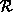 (not necessarily the same as
(not necessarily the same as 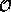 ),
),
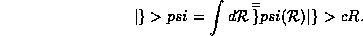
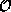 in this
representation to
in this
representation to  to produce
to produce  , and 3)
reconstruct the final quantum state from
, and 3)
reconstruct the final quantum state from  ,
,

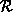 we choose, and we may thus
write (
we choose, and we may thus
write (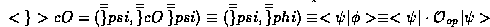

 ) in
the pure state representation associated with
) in
the pure state representation associated with 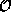 . Using the fact
that we know that the operator associated with the observable in that
representation is just multiplication by the argument we now have two
ways of writing the action of the operator on the state
. Using the fact
that we know that the operator associated with the observable in that
representation is just multiplication by the argument we now have two
ways of writing the action of the operator on the state 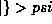 ,
,

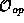 through the
integral above to conclude that for arbitrary
through the
integral above to conclude that for arbitrary  ,
,

 ,
,
 for instance, we must
have for all
for instance, we must
have for all  ,
,
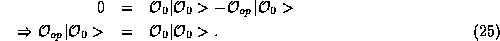
 is called the
eigenvalue (characteristic value) and
is called the
eigenvalue (characteristic value) and  is the eigenstate
(characteristic state).
is the eigenstate
(characteristic state).
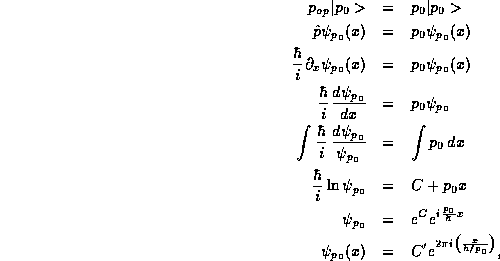
 , is
just the de Broglie hypothesis that the pure state of momentum
, is
just the de Broglie hypothesis that the pure state of momentum  is a wave of wavelength
is a wave of wavelength 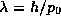 . We see that the first de Broglie
hypothesis is now built directly into our
operator framework!
. We see that the first de Broglie
hypothesis is now built directly into our
operator framework!