As physical inspiration for writing down guess solutions to (13), we recall the demonstration from lecture in which by driving the string at certain frequencies, one creates very simple motions in which all segments of the string vibrate up and down perfectly in phase and with the same frequency.
To convert the observation of these natural motions into mathematical
form, we consider the motion of the individual string segments.
During the demonstration, a segment such as that labeled 
in
Figure 1 exhibited simple harmonic motion in the
y-direction. In constructing our coordinate system, we chose the
x-axis to lay along the string while it is at rest. Therefore, the
equilibrium position of the simple harmonic motion for each segment
is 
. Hence, the motion of the particle at point
should have the form
where 
is the amplitude of the motion and 
and
are the angular frequency and initial phase, respectively. As noted
above, we observed that all points move up and down with the same
frequency and phase, with only the amplitude depending upon
the particular segment we are observing. Thus, for any
point x (not just , we may write
with the same angular frequency and phase for all points x.
Mathematically, 
gives the y-location for any value of x
and t and so actually represents a two-variable function y(x,t)
and thus a particular type of solution to the wave equation.
Converting (16) into more standard mathematical notation,
we have the mathematical definition of a standing wave or,
equivalently, a normal mode, as any solution of the form
To complete the specification of such as wave we must find appropriate functions A(x) so that (17) satisfies the wave equation (13). To do this, we substitute (17) into the wave equation. First, we evaluate the appropriate derivatives,
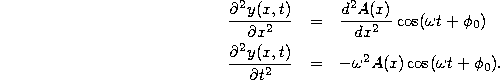
Here, we have used the facts that A(x) depends only on x, so that
x-derivatives of it are actually total derivatives and that two time
derivatives of 
turn 
into 
and
to 
while pulling out two factors of . Next,
substituting these results into (13), we find
This latter equation looks just like the equation of motion of the
simple harmonic oscillator, but with 
instead of
and zero for the equilibrium position. We already
know several forms of the general solution of such an equation.
Thus, a general solution for A(x) is
where 
is some initial phase, and we have written the
in terms of x instead of t because x-derivatives appear in
(19), and we identify the constant multiplying x as k
in direct analogue to how we usually multiply t by .
From this, we see that the angular frequency
and the wave vector k describing the standing wave always
come with the dispersion relation
From this, we at last determine the meaning of the constant c,
Thus, in a standing wave, the ratio of the wavelength to the period is
always the constant c, which for a string has the value
. From (4), we see that this constant
is precisely what we usually think of as the wave speed v.
Finally, given the general solution (20) for A(x), we now have the general form for a standing wave,
