From the definitions in Section 3.2, we can compute the
amplitude as 
and the initial phase as 
, where x(t) is given by our particular solution
(12). In both cases, we need to determine the time
at which the maximum of x(t) occurs. This we can
do by setting the derivative to zero,
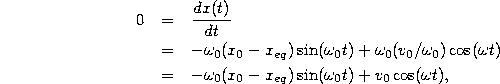
and solving for the time t,
According to our definition, the initial phase is therefore
and the amplitude is
where, in the last step, we have substituted our result (13).
Further simplification of (15) is somewhat tricky because
we must have knowledge of trig identities for 
and
. The standard trick to evaluate these is to note
that the tangent of the angle 
in Figure 3 is
x and therefore that
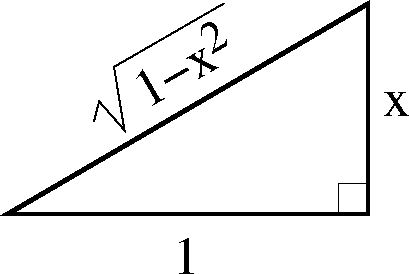
Figure 3: Right triangle for deriving trigonometric identities
Thus,
and
Substituting (17-18) into (15), we have the final result for A.
Eqs.(14) and (19) answer the question of finding
the amplitude and initial phase of an oscillator with initial position
and velocity 
. Now that we have expressions for the
amplitude and phase, some additional trigonometric identities and
transformations are worth noting. Substituting (14) and
(19) into (17) and canceling one factor of
from both sides, we find
Working similarly with (14), (19) and (18),
Substituting these last two results into the general solution, we find
an alternate form for the general solution in which A and 
are the two adjustable parameters,
