The simple form of the final results in Section 5.1, Eqs. (14,19,22), strongly suggest that there should be a simpler analysis leading to the same conclusions. That simpler analysis is the subject of this section.
For this analysis, we find yet another form of the general solution. In particular, through the use of Euler's famous formula
we may write the general solution (22) as
where 
denotes the ``real part'' of the complex
number 
. Note that throughout these notes we shall underline
variables to emphasize that they represent complex numbers.
The great utility of the complex representation is that it allows us to encode complicated trigonometric manipulations, such as those of the previous section, into familiar algebraic manipulations. For instance, we can split the exponent in (24) just as we would a real exponent,
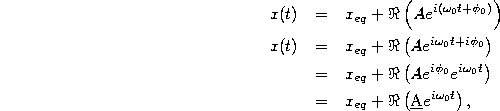
where in the last step we have combined the two real parameters of
amplitude A and phase 
into a single, handy complex amplitude
Now, to find the amplitude and phase, we repeat the general prescription for finding a particular solution from Section 4.4. We begin by expressing the boundary conditions in terms of the general solution,
and
The next step is to solve these equations for the undetermined
parameters. In this case, because we have combined both the amplitude
and phase into a single complex parameter 
, there
is only this one undetermined parameter. Now, Eq. (27)
immediately gives us the real part of ,
Finding the imaginary part is just a little more subtle. Here, and
throughout this course, when we need to talk about the real and
imaginary parts of a complex number, we shall use the subscripts r
and i respectively. Thus, we can write 
,
so that 
and
. Using this notation,
Eq. (28) becomes
Thus, we also have the imaginary part of ,
Putting both (29) and (30) together, we have the complex amplitude,
Finally, it is our job to find the real amplitude A and initial
phase given the above value for the complex amplitude
.
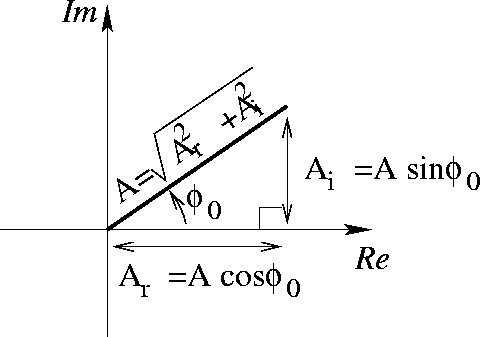
Figure 4: Argand diagram: connecting real and imaginary parts to
amplitude and phase of a complex number
To get the amplitude A and phase for any
complex number , we use Euler's formula
(23),
We see that 
is the adjacent side to angle in a
right triangle of hypotenuse A while 
is the opposite side of
the same triangle. (See Figure 4.) Thus, we may always
determine the amplitude and phase as
where we have introduced the notations 
and
for the amplitude and phase of the complex
number , respectively.
Finally, using our result for (31) and the
conversions (33), we quickly find the real amplitude
and initial phase of an oscillator with initial position 
and
initial velocity 
,
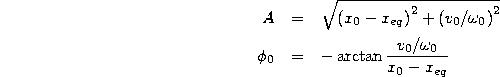
These results are exactly what we found previously (14,19), but now derived much more easily!!!
