To express conservation of energy, we need both the energy density,
which we shall call e(x), and the rate of flow of energy, which we
shall call the power 
.
The left-right rate of flow of energy across point x is the rate at
which the string to the left of point x does work on the string on
the other side of x. (See Figure 2.) The work
is the force times displacement, and so the rate of flow of energy is
force times displacement per unit time, or simply the familiar power
formula of force times velocity. The velocity is 
, and the force exerted by the string to the left of x
on the string to the right of x is, again, 
. Thus, the left-right rate of flow of energy is
For e(x), we note that energy generally consists of two forms, kinetic and potential, whose densities we shall write as ke(x) and pe(x), respectively, so that
The kinetic energy density is the kinetic energy of a chunk divided by
its length. The usual formula for kinetic energy is 
. If we divide this by the length of a chunk, the factor of m
divided by length becomes the linear mass density 
. Using the
fact that each chunk moves only along the y direction and the fact
that 
, we find
The proper form for the potential energy density is a tricky question. There is no obvious answer, and so we must return to the fundamental definition of potential energy as ``stored'' energy.
On the string, we must be careful in accounting for the energy because energy not only can be in the form of kinetic or potential energy but also can flow. Potential energy thus must be whatever is left over once we account for energy flow and kinetic energy. We now know the continuity equation as the proper way to do this accounting, and so we must find whether there is a form for pe(x) that will make the following equation true,
Note that, other than our belief that the string should conserve energy, there is no guarantee that we will be able to find a formula for pe(x) so that this equation will work. Thus, if we do find such a formula, we simultaneously accomplish two things: (a) we establish that the string does indeed conserve energy, and (b) we find the proper formula for the potential energy of the string.
To do this, we begin by taking the derivatives in (15),
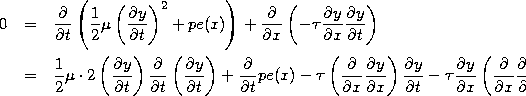
where, for the leftmost term on the first line, we used the chain rule to write the derivative of a square as twice the quantity being squared times the derivative of the quantity, and, for the rightmost term on the first line, we used the product rule to write the derivative of a product as the derivative of the first factor times the second factor plus the first factor time the derivative of the second factor. Simplifying and rearranging terms, we find
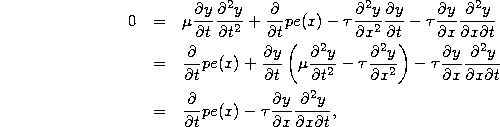
where the two terms in the large parentheses canceled as a result of the wave equation! This leaves only,
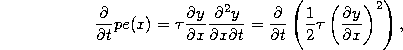
where the final, key, step on the right-hand side comes again from the chain rule for differentiating the square of a quantity. We now integrate both sides of this equation with respect to time to find
where C(x) is an arbitrary integration constant with respect to time which may depend on position.
Several comments on the above result are in order. First, we have
found a form for pe(x), which means that we have proved that energy
on the string is indeed conserved! Moreover, we find that the form of
the potential energy density is related to the slope of the string.
This is sensible because if the string is not flat, there is stored
energy: upon release, the string will start to flatten, converting the
stored potential energy into kinetic energy. It is also sensible that
the potential energy goes like the square of the slope, as either a
positive or negative slope should store the same positive amount of
energy. We also understand the dependence on 
because the
energy needed to create a given shape on the string should be in
proportion to the overall tension. Finally, the arbitrary constant
C(x) represents the usual ``arbitrary zero of potential energy'' that
one is always free to set. To keep things simple, we exploit our
freedom and choose C(x)=0, so that our final result for the potential
energy is
